BLOG DE RODRIGO CARRILLO

COMPUERTAS LOGICAS

MAPAS DE KARNAUGH

Un mapa de Karnaugh (también conocido como tabla de Karnaugh o diagrama de Veitch, abreviado como Mapa-K o Mapa-KV) es un diagrama utilizado para la simplificación de funciones algebraicas Booleanas. El mapa de Karnaugh fue inventado en 1953 por Maurice Karnaugh, un físico y matemático de los laboratorios Bell.

Los mapas de Karnaugh reducen la necesidad de hacer cálculos extensos para la simplificación de expresiones booleanas, aprovechando la capacidad del cerebro humano para el reconocimiento de patrones y otras formas de expresión analítica, permitiendo así identificar y eliminar condiciones muy inmensas.

El mapa de Karnaugh consiste en una representación bidimensional de la tabla de verdad de la función a simplificar. Puesto que la tabla de verdad de una función de N variables posee 2^N filas, el mapa K correspondiente debe poseer también 2^N cuadrados.

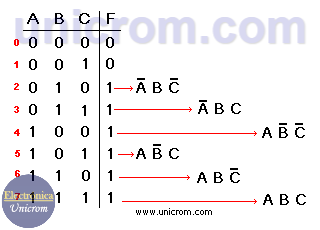
Ejemplo: Se tiene la siguiente tabla de verdad para tres variables. Se desarrolla la función lógica basada en ella. (primera forma canónica). Ver que en la fórmula se incluyen solamente las variables (A, B, C) cuando F cuando es igual a “1”. Si A en la tabla de verdad es “0” se pone A, si B = “1” se pone B, Si C = “0” se pone C, etc.

GRAFOS DIRIGIDOS

Un grafo es un modelo para representar relaciones entre elementos de un conjunto.

Gráficamente se representa como un conjunto vértices o nodos unidos por líneas que representan las aristas.

Matemáticamente, puede ser visto como un par ordenado G = (V,E) donde

V es un conjunto de vértices o nodos
E es un conjunto de pares (u,v), u,v Є V , llamados aristas o arcos que representan las relaciones entre los nodos.

En este ejemplo,

V = { a, b, c, d, e, f}
E = { (a, b), (a, c), (a, e), (b, e), (c, d), (c, e), (d, e), (e, f) }

RELACION INVERSA

En matemáticas, especialmente en análisis matemático, si f es una función que asigna elementos de I en elementos de J, en ciertas condiciones será posible definir la función f ^-1 que realice el camino de vuelta de J a I. En ese caso diremos que f ^-1 es la función inversa de f.

Sea $f$ una función real biyectiva cuyo dominio sea el conjunto $I$ y cuya imagen sea el conjunto $J$ . Entonces, la función inversa de $f$ , denotada $f^{-1}$ , es la función de dominio $J$ y codominio $I$ definida por la siguiente regla:

f(x)=y\Leftrightarrow {}f^{-1}(y)=x{\text{.}}\,\!

Destaquemos que $f^{-1}$ , al igual que $f$ , es una aplicación biyectiva, que queda determinada de modo único por $f$ y que cumple:

$f^{-1}\circ f=id_{i}$ y
$f\circ f^{-1}=id_{j}$ .

De hecho, estas dos últimas propiedades caracterizan a la función inversa, como muestra la siguiente definición alternativa.

RELACION DE EQUIVALENCIA

En teoría de conjuntos y álgebra, la noción de relación de equivalencia sobre un conjunto permite establecer una relación entre los elementos del conjunto que comparten cierta característica o propiedad. Esto permite reagrupar dichos elementos en clases de equivalencia, es decir, «paquetes» de elementos similares. Esto posibilita la construcción de nuevos conjuntos «añadiendo» todos los elementos de una misma clase como un solo elemento que los representará y que define la noción de conjunto cociente.

Ejemplos

Sea N= {0,1,2, 3...}. Se define una relación de equivalencia en NxN, como sigue: (a;b)~ (c;d) si y sólo si a+d = b +c. Esta es una relación de equivalencia en NxN y cada clase de equivalencia es un número entero. [(2;0)]= { (x;y)/ 2+y = 0 + x } a (2;0) se llama representante canónico y se denota, simplificadamente, 2.

La igualdad matemática.

La relación de congruencia módulo M en el conjunto de los números enteros (i. e. $M\in \mathbb {Z}$ ), donde se define: $a\sim b$ si y sólo si $a-b\,$ es múltiplo de M.

Esta relación es de equivalencia porque:

Es reflexiva: a - a = 0, que es múltiplo de M.
Es simétrica: si a - b es múltiplo de M, entonces b - a = -(a - b) también es múltiplo de M.
Es transitiva: sean k y l números enteros tales que a - b = M k y b - c = M l. Entonces, a - c = (a - b) + (b - c) = M k + M l = M(k + l) y por tanto un múltiplo de M. En particular, si M = 2 tenemos la tradicional clasificación de los números enteros en pares e impares.

COMPOCISION DE RELACCIONES

Composición de relaciones

Definición matemática

LA Compocision de relaciones consiste en combinar nuevas relaciones para formar otras relaciones. Sea una relación R de X en Y y una relación S de Y en Z. La composición de R y S es una relación consistente de los pares ordenados (x, z), donde x pertenece a X y z pertenece a Z y para los cuales existe un y que pertenece a Y tal que (x, y) pertenece a R y (y, z) pertenece a Z.

Queeeeee????

Vamos paso a paso

La composición se realiza entre dos relaciones llamadas, generalmente, R y S, y se denota de la siguiente manera: R ◦ S.

¿Cómo se realiza el procedimiento?

La definición nos dice que la composición se realiza a través de un par (x, y) en R y un par (y, z) en S, el resultado de estos dos es un par (x, z), mismo que se pone en la composición.

Retomando el ejemplo....

Por ejemplo: R = {(2, 1), (3, 2), (4, 3), (5, 1)}

S = {(1, 4), (2, 5), (3, 4)}

En el par (2, 1), de la relación R, x = 2, y = 1, entonces debemos buscar en la relación S pares que inicien con y para que se cumpla la condición (y, z) y como y = 1, tenemos el par en S (1, 4).

Haciendo la composición de ambos pares tenemos entonces (2, 1), (1, 4) es decir, (x, y), (y, z) el primer par de nuestra composición es (2, 4) = (x, z).

R ◦ S = {(2, 4) .... }